Christian Churches of God
[078]
Comment Déterminer le Jour de la Prochaine
Conjonction, Facilement [078]
(Édition
1.0 20020315-20041023-20061119)
Les communautés
Islamiques modernes et autrefois les communautés juives antiques ont essayé
d'estimer le moment où un premier croissant lunaire peut être visible. Avec
les anciennes listes de témoins approuvés, il s’est avéré difficile de
prévoir le jour en question et cela a rendu impossible de publier un
Calendrier Lunaire. Même avec les équipements modernes et la rapidité des
calculs disponibles, connaître de façon régulière le moment où le premier
croissant lunaire peut être vu s'est avéré être impossible. La conjonction
ne peut pas être vue. Cependant, en obtenant le nombre de centimètres qui
séparent le Soleil et la Lune au lever du soleil et en multipliant ce nombre
par 2, n’importe qui peut facilement déterminer le moment et le jour de la
prochaine conjonction.
Christian Churches of God
PO Box 369, WODEN ACT 2606, AUSTRALIA
Courriel :
secretary@ccg.org
(Copyright
ã 2002,
2004, 2006 James Dailley)
(Tr. 2006,
Rév. 2014)
Cette étude peut
être copiée et distribuée librement à la condition qu'elle le soit en
son entier, sans modifications ni rayures. On doit y inclure le nom,
l'adresse de l’éditeur et l'avis des droits d'auteur. Aucun montant ne
peut être exigé des récipiendaires des copies distribuées. De brèves
citations peuvent être insérées dans des articles et des revues
critiques sans contrevenir aux droits d'auteur.
Cette étude est disponible
sur les pages du World Wide Web à :
http://www.logon.org/ et
http://french.ccg.org/
Comment Déterminer le Jour de la
Prochaine Conjonction, Facilement
Le cycle astronomique naturel
Toute l'humanité
doit adorer le Seul Vrai Dieu, notre Père, Éloah, les jours qui sont mis à
part par le cycle astronomique naturel. La journée de vingt-quatre heures,
ou un jour de rotation solaire, commence à partir de l'obscurité, soit à la
fin du crépuscule nautique du soir, et dure jusqu’à l'obscurité à notre
heure locale (Gen. 1:5 ; Ps. 104:20). (Voir l'étude
Le Début du Mois et du Jour
(No 203)).
Les Nouvelles Lunes
se produisent à la conjonction du soleil, de la lune et de la terre. Ces
jours sont des Sabbats. Le premier jour du premier mois établit, ou fixe les
trois Fêtes annuelles avec leurs Jours Sanctifiés connexes en tant
qu’annuellement mis à part ou rendus Saints pour le culte. (Voir les études
Les Nouvelles Lunes (No 125)
;
Les Nouvelles Lunes d'Israël
(No 132)
;
Questions
Fréquemment Posées : Les Nouvelles Lunes (No 158)).
L'année commence au
printemps dans l'hémisphère nord (Ex. 12:2), avec le premier jour du premier
mois étant établi, ou mis à part à la conjonction, à l’heure de Jérusalem
(Es. 2:3).
Le mois qui est le
premier mois de l'année, est celui dont le 15ème jour arrive
après l'équinoxe du printemps. Ce jour est la Pâque, qui est catégorisée
comme une pleine lune. (Voir l'étude
Le Calendrier de Dieu (No
156)).
Plusieurs personnes
nous diront que nous avons besoin de capacités mathématiques spécialisées
pour être capables de déterminer quand les conjonctions arriveront. Toute
personne qui peut multiplier un nombre par 2 et diviser par 24 peut
déterminer le jour et l'heure de la prochaine conjonction - facilement !
La conjonction
Nous
parlerons ci-dessous de la conjonction du soleil et de la lune et de la
terre. En astronomie, la conjonction (ou être conjoint), signifie qu’il y a
une réunion de deux corps célestes ou plus dans la même longitude, ou la
correcte ascension.
On
l’appelle ‘la nouvelle lune’ lorsque la lune est située entre la terre et le
soleil et elle se nomme ‘la pleine lune’, lorsque la terre est située entre
le soleil et la lune. Cela devrait être clair à l’aide des images
ci-dessous. La nouvelle lune ne peut être visible, tandis que la pleine lune
reflète une pleine mesure de la lumière réfléchie du soleil.
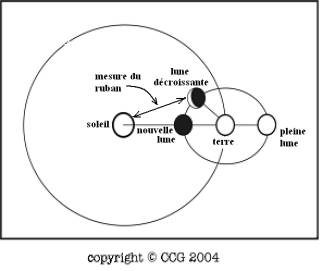
Bien que
les proportions ci-dessus soient incorrectes, l'image ci-dessus montre qu’à
la conjonction, le soleil, la lune et la terre semblent être sur une ligne
géométrique qui passe par leurs centres. Ils sont tous sur la même longitude
et nous ignorons la latitude. Au moment de la nouvelle lune, les centres du
soleil, de la lune et de la terre arrivent très près d’être alignés mais le
sont qu’occasionnellement, causant ainsi une éclipse solaire.
Le moment
de la conjonction est un temps précis partout sur la planète, selon notre
fuseau horaire local. Par conséquent, il arrive sur une période de deux
jours en utilisant l'heure locale. C'est la raison pour laquelle le jour qui
est mis à part ou rendu Saint est le jour pendant lequel le moment de cet
événement se produit dans la zone horaire de Jérusalem.
Philo d'Alexandrie
[tr. par F H Colson (Harvard University Press, Loeb Classical Library,
Cambridge, MA, 1937) ; The Special Laws (Les Lois Spéciales), II, XI, 41] écrit : "la
troisième [fête] est la nouvelle lune qui suit la conjonction de la lune
avec le soleil". Et dans II, XXVI, 140
: "Ceci est la Nouvelle Lune, ou le début du mois lunaire, à savoir la
période entre une conjonction et la prochaine, dont la durée a été
exactement calculée dans les écoles astronomiques".
On devrait noter
que l'édition populaire de l'Éditeur Hendrickson (1993), de la traduction de
1854 de C D Jonge, n'a pas la même information que donne la traduction
Colson.
Philo était un
historien juif qui écrivait au temps de Christ. Comme nous pouvons voir, les
conjonctions ont été déclarées comme étant les facteurs déterminants dans
l’établissement du premier jour du mois et non pas le croissant lunaire.
Notez qu’au temps de Christ, cette durée de temps était calculée avec
exactitude dans les écoles astronomiques.
Le livre de
Maimonides, "Sanctification of the New Moon" (La Sanctification de la
Nouvelle Lune), (Livre Trois, Traité 8, page 89, chapitre 6) écrit en 1200
EC (Ère Courante) environ, établit que :
"Le molad est
défini comme ` le moment où le soleil et la lune, dans leur mouvement
uniforme, deviennent uni dans une certaine partie du ciel, qui se produit de
la même manière partout - contrairement aux temps variables auxquels le
nouveau croissant devient premièrement visible - dans les différents
secteurs."
Cette déclaration
définit aussi la conjonction. En même temps, le Judaïsme, en général, ne l’a
pas observé et aujourd’hui, n'observe pas la Nouvelle Lune comme un Jour
Saint Sabbatique. De même que l'Islam, ils tentent de commencer le mois par
l’observation du croissant.
La conjonction
luni-solaire peut avoir lieu à tout moment pendant les vingt-quatre heures
de la rotation solaire de la terre. Comme Maimonides le fait remarquer, elle
arrive de la même manière, en même temps, partout sur la planète.
Le moment de cet
événement qui se produit pendant le fuseau horaire de vingt-quatre heures de
Jérusalem met à part ce Jour de la Nouvelle Lune à la conjonction en tant
que Sabbat (Amos 8:5 ; Es. 66:20-23 ; Ez. 46:3 ; Ps. 81:3 ; Col. 2:16).
Cette étude est
importante afin que tous puissent apprendre à déterminer facilement
n'importe quel futur Jour Saint de Nouvelle Lune, si les données publiées ne
sont pas disponibles.
La précision avec
laquelle cet événement pouvait être prévu, permettait à la communauté marine
et aux forces navales d’évaluer leurs arrivées et départs. C'est important
pour eux parce que les cycles de la lune gouvernent les marées de l'océan.
Dans le monde
entier, la conjonction se produit le jour qui commence le nouveau mois
astronomique.
Le fait est que
nous sortons d’un âge des ténèbres
induit par les Trinitaires. Les partisans du Christianisme Trinitaire ont
intentionnellement enlevé la majeure partie de la connaissance que les gens
avaient des temps anciens.
Le livre,
Maps of the Ancient Sea Kings
(Cartes des Rois Marins Antiques),
1966, par Charles Hapgood, est une référence utile. Il montre et explique
plusieurs cartes et registres antiques d'Alexandrie. Il explique la vaste
connaissance géographique détaillée, et la compréhension de la navigation
que les peuples antiques possédaient.
Tous les peuples
navigant et pêchant partout sur la terre ont compris cette synchronisation
luni-solaire et la relation entre la marée et le trajet de la lune. C'est
seulement récemment que les gens ont généralement abandonné cette
connaissance qui était également nécessaire pour le voyage.
Le cycle lunaire
Le trajet quotidien
apparent de la lune autour de la terre prend 24 heures et 50 minutes. Cela
cause la montée et la descente des océans à des intervalles assez réguliers.
En moyenne, la période entre deux hautes marées successives est de 12 heures
et 25 minutes, ou la moitié du temps que prend la lune pour circuler autour
de la terre. Les marées de l'océan sont causées principalement par
l’attraction gravitationnelle de la lune.
À la conjonction,
la lune est alignée avec le soleil de l'extérieur de notre point de vue sur
la terre. Nous voyons le côté sombre de la lune, ou plutôt nous ne voyons
pas la lune du tout parce que la brillance extrême du soleil nous éblouit et
nous empêche de voir la lune extrêmement terne.
Une nouvelle lune
se produit quand les longitudes apparentes de la lune et du soleil diffèrent
de 0°.
À mesure que la
lune se déplace vers l'est en s’éloignant du soleil dans le ciel, nous
voyons un peu plus de son côté ensoleillé chaque nuit. Alors, quelques jours
après une nouvelle lune, nous pouvons voir en soirée un mince croissant dans
le ciel à l'ouest. À ce point, et durant les nuits suivantes, nous pouvons
voir le côté sombre de la lune faiblement illuminé par la lumière du soleil
reflétée par la terre.
Le premier quartier
de la lune est le croissant de lune qui continue à s’accroître ou à
s'agrandir de plus en plus. Quand la moitié du disque de la lune est
illuminée, nous disons que la lune a atteint la phase du premier quartier.
Ce terme vient du fait que la lune est à un quart du cycle de la
lunaison.
Au premier
quartier, la lune est à 90 degrés à l'est du soleil le long de l'écliptique,
ainsi nous regardons le côté ensoleillé de la lune de côté. A ce moment-ci,
50 % de la surface visible de la lune est illuminé. Parce qu’elle est à 90
degrés du soleil, le premier quartier de la lune se trouve approximativement
au milieu de la nuit.
La lune gibbeuse
grandissante continue à s’accroître (grossir), mais elle n’est plus un
croissant. Pendant cette période après le premier quartier, nous disons que
nous avons une lune gibbeuse.
La pleine lune est
à l’opposé du soleil dans le ciel et nous voyons tout le côté ensoleillé de
la lune. La pleine lune est à 180 degrés autour de l'écliptique du soleil
dans le ciel. A ce moment-ci, 100 % de la surface visible de la lune est
illuminé.
Elle se
lève presque exactement au moment que le soleil se couche et elle se couche
presque en même temps que le soleil se lève le matin suivant.
La deuxième moitié
du trajet de la lune est l'inverse de la première. Maintenant, la lune
décroît, ou devient plus petite et elle est encore une fois de plus
qualifiée de gibbeuse.
Une lune
gibbeuse décroissante est la deuxième moitié du trajet de la lune et
est l'inverse de la première. Chaque soir, elle se lève de plus en plus
tard, après le coucher du soleil.
La lune du
troisième quartier est au trois-quarts de son trajet et la lune nous montre
de nouveau un côté de son disque illuminé et l'autre dans l'obscurité.
Cependant, le côté illuminé que nous voyons est maintenant celui qui était
dans l'obscurité à la phase du premier quartier.
Le dernier quartier se produit
lorsque les longitudes apparentes de la lune et du soleil diffèrent de 270°.
A ce moment-ci, 50 % de la surface visible de la lune est illuminé.
La lune se lève
vers minuit et traverse le méridien local vers le lever du soleil. À mesure
qu’on s'approche de la nouvelle lune, la phase de la lune est un croissant
qui décroît jusqu'à ce que nous ne puissions plus la voir du tout. Elle
devient alors une nouvelle lune et ainsi le cycle recommence.
Nous ne verrons pas
beaucoup le dernier croissant de Lune après environ 28 jours. Nous ne voyons
rarement le nouveau croissant de lune qu’après un âge de plus de 24 heures.
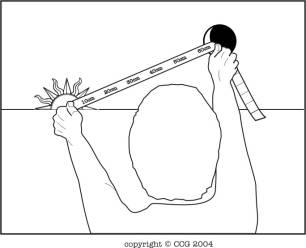
Comment calibrer le Ruban à Mesurer
Nous devrions tenir
un ruban à mesurer à bout de bras, directement devant notre visage.
Typiquement, la distance entre nos yeux et le ruban à bout de bras est
environ de 60 centimètres pour l'adulte moyen.
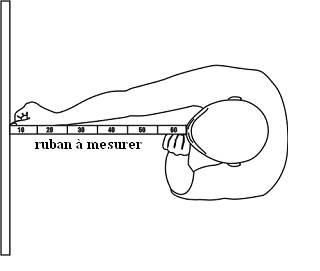
Afin de calibrer le
ruban à mesurer pour la taille de notre corps, nous nous tenons face à un
mur et mesurons 60 cm entre nos yeux et le mur. Si nous avons des bras longs
ou courts, nous aurons besoin d'ajuster étant donné que cette mesure est
importante pour mesurer les degrés et donc le temps mesuré selon la
distance ; la distance entre le soleil et la lune dans notre cas.
À cette distance,
une division de centimètre sur le Mètre équivaut à un angle de 1/60 radians.
Puisqu'un degré est équivalent à 1/57.295 radians, l'angle sous-tendu par un
objet de 1 cm à bout de bras est une approximation tout à fait raisonnable
de 1 degré astronomique. Par exemple, le diamètre apparent de la pleine lune
serait environ 0,5 cm lorsque mesuré avec un ruban à mesurer à bout de bras.
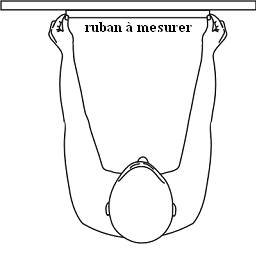
Tenir le ruban à
plat contre le mur avec les deux mains à cette distance de 60 cm. Ajustez
les mains, bras, épaules, hanches et le cou de sorte que vous puissiez
toucher le mur avec le ruban à plat mais vos yeux restent à la distance
originale de 60 cm. Rappelez-vous de cette position pour fin de précision en
effectuant la mesure entre le soleil levant et la lune décroissante.
Les angles peuvent
être évalués à une approximation raisonnable en tenant une règle à bout de
bras, ou en utilisant la main.
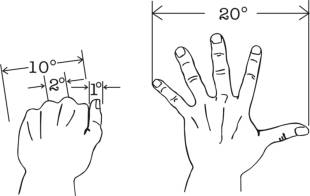
Un poing serré (le
pouce exclus) couvre environ 10 degrés tandis qu'une main pleinement ouverte
couvre environ 20 degrés, de la pointe du pouce à la pointe du petit doigt.
Pour des angles plus petits, nous pouvons utiliser d'autres méthodes
indicatives. Par exemple, à bout de bras, la largeur de notre plus petit
doigt équivaut à approximativement un degré. La largeur du pouce face à nous
équivaut environ deux degrés et de côté équivaut à un degré et la distance
entre le pouce et sa première jointure est environ trois degrés.
Bien que les mains
et les bras de chacun soient différents, bien sûr, il est encore assez
facile de prendre nos propres mesures de la longueur de nos bras, de la
largeur de main et ainsi de suite et de calibrer nos propres guides naturels
pour nous aider à estimer les angles dans le ciel.
Adapté d'un article d’un magazine d'Astronomie
(britannique) par Iain Nicolson.
Les images
ci-dessous nous aideront à comprendre le concept actuellement discuté.
Souvenez-vous, un
centimètre est égal à un degré de mouvement astronomique.
Ce mouvement
astronomique de la lune prend près de deux heures.
Dans l'hémisphère
nord, l'Étoile Polaire, Polaris, est toujours en ligne avec les deux étoiles
sur l'extérieur de l’ourse. Ceci est le vrai nord et cela peut facilement
être vu dans l'image ci-dessous et avec un peu de pratique peut être
facilement localisé.
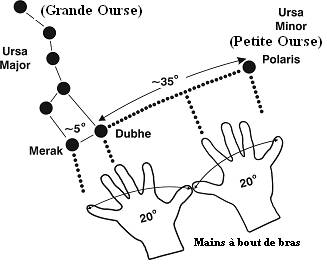
Pour notre revue,
le concept peut facilement être compris si l'angle (montré en degrés), entre
le soleil au lever et la lune à n’importe quel jour de son dernier quartier
est utilisé au lieu de Polaris et Merak.
Comment déterminer le jour
Pour nos besoins,
nous utiliserons un ruban de un mètre (100 centimètres), étant donné que ce
n’est pas coûteux et facile à transporter. Son utilisation ne requiert pas
beaucoup de pratique, juste une bonne météo et une bonne vision.
Quand le soleil se
lève, prenez la mesure en centimètres entre le centre du soleil et le centre
de la lune décroissante. Enregistrez la date du jour et l'heure locale
correcte à la minute et le nombre de centimètres indiqué.
La lune se déplace
presque 0,5 cm par heure, donc nous multiplions le nombre de centimètres
indiqué par 2. Cette mesure nous donnera le nombre approximatif d'heures,
que nous devons convertir en nombre de jours jusqu'à la conjonction
suivante.
Nous le faisons en
divisant le susdit nombre de centimètres par 24 heures pour fournir le
nombre de jours entiers. Ajoutez ensuite le nombre d’heures restantes et
nous connaîtrons à quel jour et quelle heure locale approximative la
Nouvelle Lune suivante se produira.
Cette mesure peut
être faite n'importe quand après la pleine lune, mais durant le troisième
quartier avec 7,4 jours restants jusqu'à la conjonction, cela est plus
facile.
Les 7,4 jours sont
équivalents à 177 heures et 36 minutes. Sept jours entiers sont 168 heures
et 0,4 de 24 heures est 9 heures et 36 minutes.
Cette mesure nous
donnera le nombre d'heures que nous devons convertir en nombre de jours
jusqu'à la prochaine conjonction à notre heure locale. Si cela place la
conjonction près de la noirceur à Jérusalem, alors faites les calculs
ci-dessous, c’est à dire diviser par 0,51°, pour obtenir un résultat plus
précis.
Pour la plupart des
jours, multiplier par 2 est satisfaisant.
La lune se déplace
relativement au soleil d’une quantité presque égale au diamètre de la lune à
chaque heure, ce qui égale 0,51° ou 0,5 cm. Ceci équivaut environ à un
mouvement de 12,2° à chaque jour de vingt-quatre heures, pour le trajet
mensuel.
L'utilisation d'un
ruban en centimètres nous fournit une estimation très précise, mais même
l'utilisation de nos doigts nous fournira une approximation remarquablement
précise.
La division par un
taux de changement de 0,51° par heure nous fournira un résultat plus précis.
C'est un peu moins (une ou deux heures de moins) que simplement multiplier
par deux. Si la multiplication par 2 place la conjonction près de la fin du
jour près de la noirceur, la fin du crépuscule nautique du soir (FCNS),
alors faites les calculs pour obtenir le résultat plus précis nécessaire.
Le taux de
changement par heure sera égal à l’heure de la future conjonction, en
heures, à partir du temps où nous avons pris nos mesures.
Nous devons ajuster
cette heure locale de la conjonction à l’heure de Jérusalem et ajuster le
jour si requis.
Ceci est fait afin
que toutes les Églises de Dieu actuellement, et éventuellement toute
l'humanité, observent un jour uniforme d'adoration sur notre planète ronde.

Ci-dessus est une
image de la lune avec croissant le 14 avril 2004 à l'heure locale 06:46 au
sud de l'Ontario, Canada. Le lever du soleil était à 06:40, heure ajustée
d’été, qui avait commencé le 4 avril à 02h00, ajoutée. C'était le jour 24 du
cycle, avec une lune décroissante durant la phase du troisième quartier.
La lune a été
pleine le 5 avril à 06h03, heure locale. Après l’obscurité, durant la soirée
du 4 avril était le 15ème jour du premier mois. C'est la Soirée
Mémorable ou la nuit du Repas actuel de la Pâque. Le moment du dernier
quartier de la lune était le 11 avril à 10:46 en soirée et la lune devait
être nouvelle à 08h21 heure locale, le 19 avril 2004.
Cet événement a eu
lieu à 13:21 GMT, qui est 15h21 ou 3h21 PM dans le fuseau horaire de
Jérusalem. Ceci est une différence de sept heures dans l’heure du jour
versus l’heure locale, mais durant le même exact jour de la semaine.
L'information
lunaire est publiée par
http://aa.usno.navy.mil/data/docs/MoonPhase.html#y2004
La mesure sur le
ruban a été évaluée à 62 centimètres. 62 x 2 indiqueront 124 heures. 124
divisé par 24 (heures) donne 120 heures pour cinq jours complets avec 4
heures restantes. L'addition des 4 heures à 06:46 nous donne une estimation
10:46 le 19 avril pour l'heure locale prévue de la conjonction. Ceci est 2
heures 25 minutes plus tard que le temps publié, mais clairement durant le
jour correct.
Si nous avions
besoin d'un temps plus précis alors nous diviserions 62 par 0,51. Cela nous
donne 121,6 heures. Cela signifie que nous ajoutons 1 heure 36 minutes à
06h46 et obtenons 08h22, soit une minute de retard à comparer aux temps
publiés de la prochaine conjonction.

Les images
du soleil et de la lune avec croissant ci-dessus sont exagérées pour être
vues plus facilement.
Plus grande est la
distance angulaire entre la Lune et le Soleil, plus nous pouvons voir le
côté illuminé de la Lune. Une lune avec un croissant très mince indiquerait
que seulement quelques jours restent jusqu'à la Nouvelle Lune.
Contexte
La mesure angulaire
signifie n'importe quelle mesure de la séparation de deux objets tel que vus
d'un point spécifique. Elle est exprimée en unités angulaires (degrés,
minutes d'arc, ou secondes d'arc).
Les mesures
angulaires sont utilisées par les observateurs astronomiques pour décrire
les positions des objets célestes dans le ciel. Pour nos besoins, ces objets
sont le Soleil et la Lune et leur séparation angulaire telle que vue de la
terre durant le dernier quartier de la lune. Ceci est mesuré en degrés de
séparation.
Quand la distance
angulaire est d’une séparation de moins de 90°, nous verrons moins que la
moitié du côté illuminé de la lune. Elle ressemblera à une petite tranche
incurvée illuminée et elle est appelée la phase du croissant décroissant.
Le nombre de ces
degrés entre le soleil levant et la lune décroissante équivaut à une durée
en heures qui restent jusqu'à la prochaine conjonction.
Pour des
estimations approximatives qui doivent être utilisées pour estimer le temps
restant jusqu'à la prochaine conjonction, les règles largement reconnues
sont très simples. Elles sont aussi étonnamment précises dans l'estimation
du jour de la prochaine conjonction.
À mesure que plus
de temps est passé à observer le mouvement de la lune dans le ciel, comme le
faisaient les anciens, nous serions familiers avec les différents cycles du
mouvement de la lune. Nous serions alors en mesure de connaître plus
exactement à quels points dans ses cycles la lune se déplace plus rapidement
ou plus lentement que la moyenne de 29,53 jours par mois.
Nous utiliserions
ces chiffres modifiés pour déterminer l’heure de conjonction très
précisément, comme les anciens étaient en mesure de l’obtenir.
Des mathématiques
simples, soit diviser par 0,51, seront seulement exigées quand le temps de
la conjonction est près de l'obscurité, à la fin du crépuscule nautique du
soir, FCNS.
Le reste du temps,
nous devons simplement multiplier la séparation angulaire par deux.
Anciennement,
Aristarchus a également déterminé l'angle entre la phase de quartier de Lune
et le Soleil.
Aristarchus de Samos
Aristarchus
de Samos (environ 310 EC) dans son livre "On the Sizes and Distances of the
Sun and Moon (Sur les Dimensions et les Distances du Soleil et de la Lune)"
a essayé de déterminer la distance relative entre la Terre et le Soleil en
remarquant à partir de la géométrie simple que Terre-Lune-Soleil formaient
un triangle droit avec l’angle de 90 degrés à la position de la Lune lorsque
la lune était à la phase du quartier (1/2 de son disque illuminé par le
Soleil).
Cela signifie
que si vous pourriez mesurer l'angle de la Lune-Terre-Soleil, vous pourriez
établir ce qu’était la longueur relative de l'hypoténuse de ce triangle
entre la Terre et le Soleil, en termes de longueur de la distance de
Lune-Terre. Le problème est que cet angle est très près de 90 degrés et est
en fait environ 89 degrés. Même une erreur de 1 degré sur un tel triangle si
mince crée une erreur assez importante.
Alors,
comment Aristarchus a-t-il mesuré cet angle ?
Il a essayé
de mesurer l'intervalle de temps entre le premier et le troisième quartier
de Lune et a calculé leur différence qui par la géométrie de la situation
vous donnerait deux fois l'angle Lune-Terre-Soleil.
Le problème
est que bien que ceci fonctionne en principe, l'orbite de la Lune n'est pas
circulaire et la Lune ne voyage pas à une vitesse constante.
Ces facteurs
ont mené Aristote à obtenir une distance de 18-20 fois la distance de la
Terre-Lune comme étant la distance au Soleil au lieu de (93 million/240,000)
= 3900.
1997 Dr. Sten
Odenwald
Estimation des Angles à l'Œil
Comme nous avons vu
susdit du travail d'Aristarchus de Samos, la mesure angulaire a été
anciennement utilisée et a été comprise et utilisée par tous.
Aujourd'hui, elle
est utilisée par des astronomes aussi bien que par des navigateurs.
Si Aristarchus
avait eu des outils de mesure plus précis, il aurait eu une projection plus
proche, mais cet exemple montre que le concept était compris.
Tous sont plus ou
moins familiers avec les horloges solaires. Possiblement la plus précise de
toutes les horloges de type solaire antiques est l’horloge à 'étoile'. Elle
est appelée l’horloge Nocturne.
Elles ont été
utilisées dès le 15ème siècle par des navigateurs, qui
déterminaient l'heure par la position des étoiles, aussi bien que par le
mouvement du soleil et de la lune.
L’horloge Nocturne
fonctionne si bien dans l'hémisphère nord parce qu’elle est basée sur
l'Étoile Polaire, qui est appelée Polaris.
Polaris se situe
presque directement sur l'axe de l’inclinaison de la terre et apparaît
toujours dans la même position dans le ciel.
La Grande Ourse
tourne en un cercle complet autour de l'étoile polaire, Polaris. Par
conséquent, chaque fois que nous cherchons l'Étoile Polaire, l’Ourse, quelle
que soit sa position occupée dans le ciel, indiquera correctement Polaris.
Ceci est fait en
utilisant les deux étoiles extérieures de l’Ourse, Merak et Dubhe et les
alignant avec l'Étoile polaire.
Cela n’est pas très
utile aux gens vivant dans l'hémisphère sud mais l’explication est tout à
fait claire.
L'alignement montré
dans l'outil ci-dessous doit être compris dans notre heure locale.
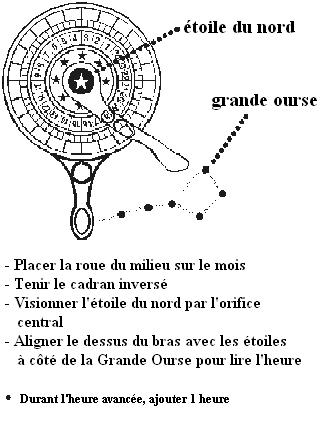
Angles du Soleil, de la Terre et de
la Lune
Une façon
d’enregistrer graphiquement le comportement de la Lune est de tracer sa
position par rapport au Soleil et la Terre. Spécifiquement, nous pouvons
mesurer l'angle entre la Lune et le Soleil, avec la Terre comme le sommet de
l'angle. À un moment où la Lune et le Soleil sont visibles, nous pouvons
mesurer l'angle entre la Lune et le Soleil à partir de notre emplacement
d'observation. Chaque fois que nous mesurons et enregistrons l'angle, nous
devrions aussi observer et enregistrer la forme (la phase) de la Lune et
remarquer si la partie éclairée ou non éclairée de la Lune est la plus
proche du Soleil.
Les durées ou âges
durant les phases du cycle lunaire montrent qu'un cycle complet prend
environ 29,53 jours. Le mois synodique et la durée ou âge de la lune dans
n'importe quelle phase sera toujours moins de 30 jours.
Le premier quartier
correspondra à une durée ou âge d'environ 7,4 jours, la pleine lune à
environ 14,8 jours et le troisième quartier à environ 22,1 jours. Cela
laisse environ 7,4 jours jusqu'à la conjonction.
7,4 jours sont sept
jours et 0,4 x 24 = 9,6 heures et 0,6 x 60 = 36 minutes. Cela indiquerait
qu’à partir du troisième quartier, il y aura 7 jours 9 heures et 36 minutes
jusqu'à la prochaine conjonction.
Quelques Définitions
Altitude
est la mesure en degrés de la séparation angulaire d'un objet céleste
au-dessus de l'horizon.
Azimut
est la mesure en degrés de la position d'un objet céleste autour de
l'horizon à partir du Nord.
FCNS est
la fin du crépuscule nautique du soir.
Ellipse
est une forme ovale régulière, tracée par un point se déplaçant dans une
surface de manière que la somme de ses distances de deux autres points soit
constante.
Horizon
est le cercle autour d'un observateur où le ciel et la terre se joignent. Un
objet céleste peut seulement être vu s'il est au-dessus de l'horizon.
Latitude
est la distance angulaire d'un endroit au nord ou au sud de l'équateur de la
terre, ou de l'équateur d'un objet céleste, d'habitude exprimé en degrés et
en minutes.
Longitude est la distance angulaire d'un endroit à l’est ou à l'ouest du méridien de
Greenwich, ou à l'ouest du méridien standard d'un objet céleste, d'habitude
exprimé en degrés et en minutes.
Lunaison
est une autre expression pour un mois lunaire.
Le Méridien est la ligne à travers le ciel qui croise l'horizon directement au nord de
l'observateur, et s'étend par le méridien et rencontre l'horizon de nouveau
à un point directement au sud de l'observateur.
Le Radian est une unité d'angle, égal à un angle au centre d'un cercle dont l'arc est
égal en longueur au rayon.
Le Zénith
est le point dans le ciel directement au-dessus de la tête de l'observateur.
L'Application Pratique
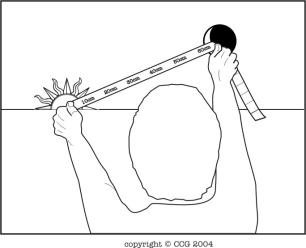
Quand le soleil se
lève, utilisez un ruban de 100 centimètres pour mesurer en centimètres la
distance entre le centre du soleil au lever et le centre de la lune
décroissante au sud-est.
Enregistrez la date
du jour et l'heure locale exacte à la minute et le nombre de centimètres
montrés.
Multipliez ce
nombre de centimètres par deux pour obtenir un nombre approximatif d'heures
jusqu'à la prochaine conjonction dans l'heure locale. Cette mesure nous
donnera le nombre approximatif d'heures que nous devons convertir en nombre
de jours, jusqu'à la prochaine conjonction.
Divisez le nombre
d'heures par 24 pour avoir le nombre entier de jours restants. Ensuite
additionner les heures restantes et nous saurons quel jour local et à quelle
heure locale approximative la prochaine Nouvelle Lune se produira.
Convertissez cette
heure locale à l’heure de Jérusalem et vous saurez quel jour est le prochain
jour de la Nouvelle Lune Sabbatique.
Reconnaissance :
Merci à Norman Gray pour les illustrations, qui sont à des fins uniquement
conceptuelles, et à Kirk Woodside pour sa contribution.
q